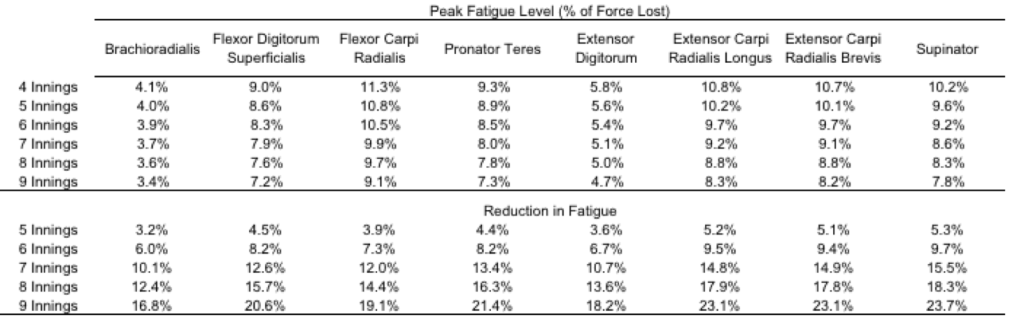
As previously mentioned, there really isn’t anything better than getting your hands on new data. That new data smell, the excitement of telling someone that the singular of data is datum. I was really excited to see a follow up study (O’Connell, Hart & Boddy, 2016) to the Bauerfeind study that examined the influence of pitch velocity on arm stress (O’Connell & Boddy, 2016). After reading the article, there were some really surprising findings that I wanted to look into further. More specifically – the claim this study replicated the findings of Post et al (2015), and found a non-significant relationship between elbow valgus torque, and ball velocity.

The study can be found here:

https://www.drivelinebaseball.com/elbow-stress-motus-sleeve-velocity/

But, here are some of the key findings.

• A “very small” relationship between the stress metric, and pitch velocity of r² = 0.21
• “This contradicts a commonly believed hypothesis that when comparing pitchers across a population the ones who throw the hardest also experience the greatest stress. We are only looking at elbow stress, this may not hold up when looking at both elbow and shoulder stress. But this is a very interesting finding nonetheless!”

First of all, I wanted to look at simply the interpretation of these data. The r² statistic infers how much of variable A can we infer from variable B. For example, if our r² value is 0.5, that represents that variable B accounts for 50% of the variation in variable A. When studying human movement, Vincent and Weir (2012) proposed threshold values of r2 = 0.25 to 0.49 as low, 0.49 to 0.64 as moderate, and greater than 0.81 as strong. However, they included this caveat:

“Values lower than (0.25), if they are statistically significant, can be useful for identifying nonchance relationships among variables, but they are probably not large enough to be useful in predicting individual scores. However, in conjunction with more than one predictor variable (multiple regression)… even individually modest predictors may be useful”

– Vincent & Weir, 2012, page 117.

The values reported in their text are r values, but I have adjusted them to be r² values.

So, let’s look at these results – a “very small” relationship, and “similar to the findings of Post et al., 2015”. Post et al (2015) found

“very small r² values, indicated that very little of the variance in joint kinetics can be explained by ball velocity… the correlations between ball velocity and both elbow-valgus torque and shoulder external-rotation torque were not significant”

The values reported by Post et al (2015) were an r² of 0.04, and p=0.053, or, 4% of elbow valgus torque could be explained by ball velocity, and this relationship was not statistically significant. This is where I have some concerns with the interpretations of the newest study from O’Connell and Boddy (2016). Their study reveals a statistically significant relationship between ball velocity and arm stress, in the low range of correlational strength (r² = 0.21).  Interpreting these results in their current form, these findings indicate that 21% of arm stress can be predicted using ball velocity alone. So, ignoring any differences in mechanics between pitchers, fatigued state, or pitcher body size, we already have a model that predicts 21% of our dependent variable. As someone who has spent a good amount of time wrestling with data, attempting to prove hypotheses about muscle fatigue, I would typically kill for a relationship with this strength! The findings of the O’Connell & Boddy study do not replicate those of Post et al., 2015 – they illustrate a link between arm stress and pitch velocity – and that is without moving on to some methodological concerns.

The beauty of blogging, and posting open source data to try and further science, is that you live in a state of constant, dynamic, peer review. In many ways, this is vastly superior to the traditional publication model, where studies are reviewed by academics, then go to sit on bookshelves and are never looked at again. When open data is published, it gives others a chance to chime in on the results.

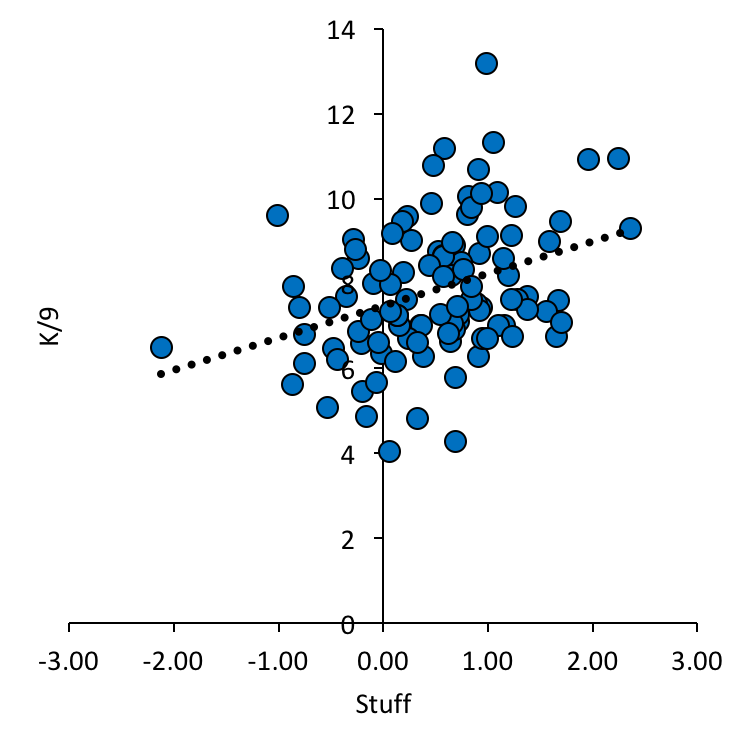
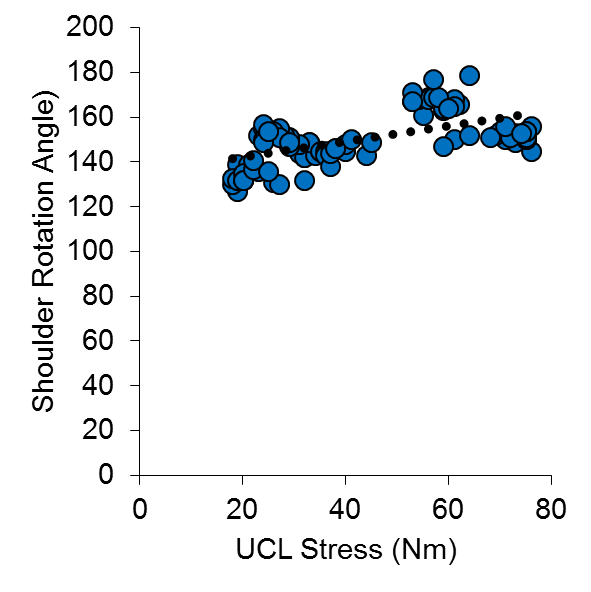
Looking at the data that went in to calculating the r² value of 0.21 between stress and velocity, a couple of things emerge. First of all, not all pitchers have the same contribution to the means. Two pitchers only threw 6 pitches, while one threw 19 pitches. If pitch velocity only indicates 21% of the variance in arm stress, there are clearly other factors at play. If we have an unequal number of pitches between our participants, we’re leaving room for error, by having someone with greater stress contributions from other variables swaying our correlation, one way, or the other. To try and accommodate for this, I removed the two pitchers from the analysis who only threw 6 pitches. I then took the average velocity, and stress, from the top 9 velocity throws from all other pitchers, and put them into the correlation with an n=15. The correlation between velocity and stress now goes up to r² = 0.32, or 32% of the variance in arm stress is accounted for by ball speed. Including all of the pitches individually, and only using the top 9 pitches from each pitcher (an n=97), we end up with a correlation of r² = 0.37 between velocity and arm stress.

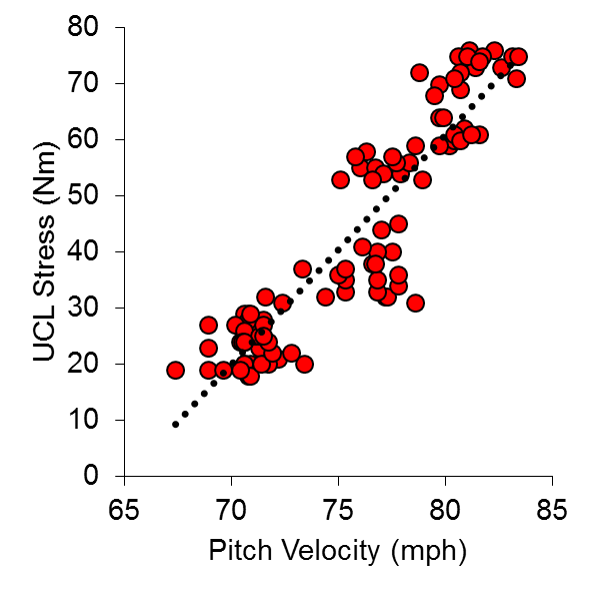
When your model can account for 37% of the variance between one variable and another, you are definitely on to something. This is statistically significant, and when visualized (Figure 1), it becomes quite clear that a relationship exists. In fact, this number appears to be nearly an exact replica of another study, where Hurd et al., (2012), found a relationship of r² = 0.37 between pitch velocity and elbow adduction moment.

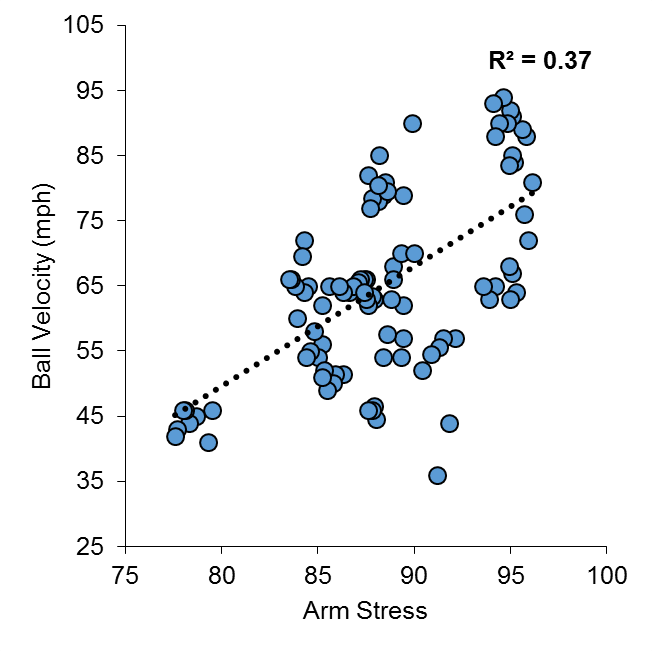
Figure 1 Correlation between Arm Stress and Ball Velocity, for top 9 velocity throws (n = 15 pitchers, 97 pitches)

So, what about the other variables that the Motus sleeve spits out? I can’t tell you with 100% certainty what arm slot, or shoulder rotation means from these data, but I included ball speed, arm speed, arm slot, and shoulder rotation, in a multiple linear regression model to predict Stress. Once again, I used the top 9 velocity pitches from 15 pitchers to do this analysis.

To put all of the variables on the same scale, I converted them all into z-scores – this will give us standardized coefficients that we can compare against one another in our regression output.

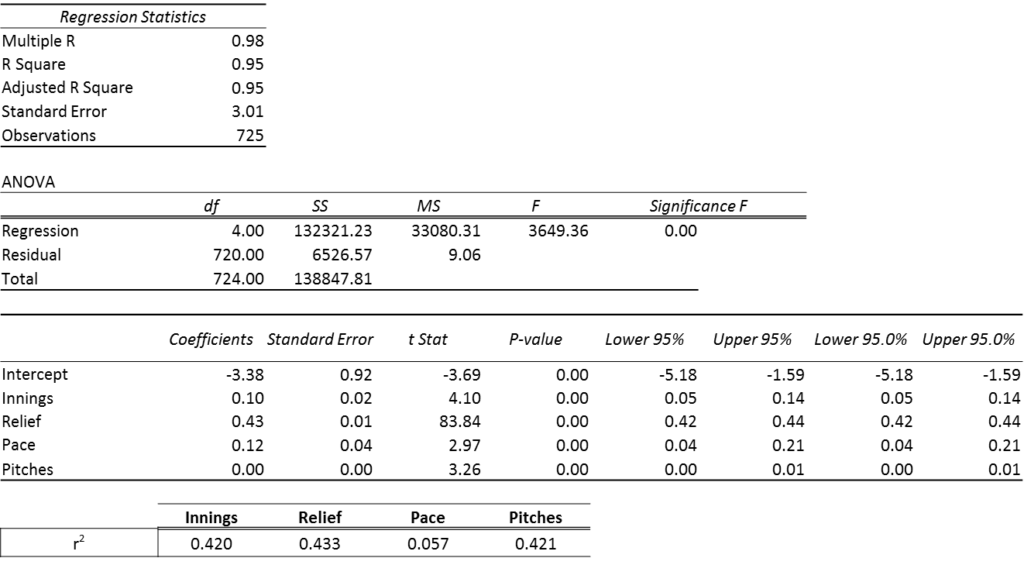
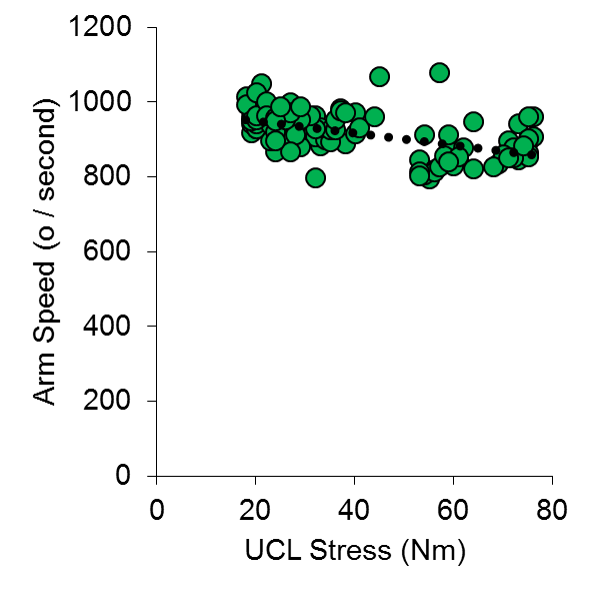
In summary, this model produced an r² value of 0.55, with Arm Slot and Shoulder Rotation not being the weakest predictors of arm stress, and arm speed having a negative relationship with arm stress (Figure 2).

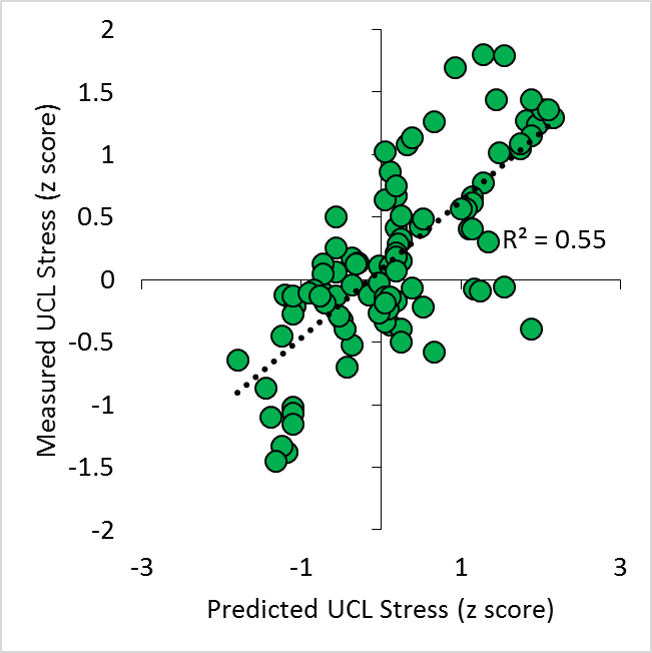
Figure 2. Predicted and actual UCL stress (z scores), from input variables of ball velocity, arm slot, arm speed, and shoulder rotation.

It is quite clear that there are other variables not being measured that will help produce a better model of arm stress, but from the main predictor of arm stress right now remains ball velocity. These data collected using the Motus Sleeve, on one of the more advanced populations of pitchers that have been researched, echoes many of the findings that Hurd et al., (2012) produced in a lab setting. It is important to understand how statistics are interpreted, and what assumptions go in to calculating results.

This study goes deeper into understanding the stress on the arm during pitching (as this is tracked from actual bullpen sessions, and not flat ground throws like in the Bauerfeind study). Other studies that have examined the risk of UCL injury in youth pitchers, have identified fatigue, stature, and cumulative pitch effects as risk factors for injury (Chalmers et al., 2015).

Conclusion

In summary, pitch velocity shows a significant relationship with arm stress, using the Motus Sleeve. If you throw harder, chances are, you will have higher levels of stress on your UCL. It is important to properly condition and be strong, so you can withstand these stresses. There are many other factors that go in to determining just how much stress is on the UCL, but these must be further studied by hard working groups like Driveline, and researchers in other facilities.

Here are the data I used for the analyses above.

References

Chalmers, P. N., Sgroi, T., Riff, A. J., Lesniak, M., Sayegh, E. T., Verma, N. N., … & Romeo, A. A. (2015). Correlates with history of injury in youth and adolescent pitchers. Arthroscopy: The Journal of Arthroscopic & Related Surgery, 31(7), 1349-1357.

Hurd, W. J., Jazayeri, R., Mohr, K., Limpisvasti, O., ElAttrache, N. S., & Kaufman, K. R. (2012). Pitch velocity is a predictor of medial elbow distraction forces in the uninjured high school–aged baseball pitcher. Sports Health: A Multidisciplinary Approach, 4(5), 415-418.

O’Connell, M., Hart, S., & Boddy, K. (2016). Elbow Stress, Motus Sleeve, and Velocity. Retrieved from https://www.drivelinebaseball.com/elbow-stress-motus-sleeve-velocity/, November 4, 2016.

O’Connell, M., & Boddy, K. (2016). Can You Reduce Pitching Elbow Stress Using a Sleeve? Retrieved from https://www.drivelinebaseball.com/can-reduce-pitching-elbow-stress-using-sleeve/, November 4, 2016.

Post, E. G., Laudner, K. G., McLoda, T. A., Wong, R., & Meister, K. (2015). Correlation of shoulder and elbow kinetics with ball velocity in collegiate baseball pitchers. Journal of athletic training, 50(6), 629-633.

Sonne, M.W. (2016). UCL Stress and Velocity Increases. Retrieved from http://www.mikesonne.ca/baseball/ucl-stress-and-velocity-increases/, on November 4, 2016.

Vincent, W., & Weir, J. (1999). Statistics in kinesiology. Human Kinetics. Champagne, Illinois.

Well, now that we know what Brandon Morrow’s stuff looked like with the Jays in 2010, let’s move on to understanding pitcher workloads since 2007.

First – a foray back into my thought process for the days of rest penalty in the metric. If you look back to the second article on Cumulative FU’s, I proposed that for consecutive day appearances, the FU’s be multiplied by 5. For 2 to 4 days of rest, the FU’s were multiplied by 2. For the standard, every 5th day – there was no multiplier for the FUs.

When I looked at the predicted FU’s for all pitchers (and as you’ll see shortly), the high use relievers – 80-100 innings in a season – had the highest workloads – significantly higher workloads than starters for the most part. I thought, I may have to make an adjustment to the metric – but I wanted to look at starter vs. reliever injury rates first.

I downloaded Jon Roegele’s Tommy John Surgery (TJS) list (@MLBPlayerAnalys), and then classified pitchers as relievers (if 80% of more of their innings came from relief innings), or starters. I compared numbers from the 2007 to 2016 seasons. Only pitchers who pitched 10 innings in a season were included in the analysis.

I looked at the sum of innings pitched and the number of TJS that occurred for all pitchers, and came up with a ratio of innings per TJS, for both starters, and relievers.

There were a total of 125092 innings pitched by Relievers during this time period, and 290401.1 innings pitched by starters. During that time, 151 relief pitchers required TJS, and 141 starters required surgery. This worked out to a ratio of 848.4 innings per TJS for Relievers, and 2059.6 innings per TJS. These data should likely be vetted a bit more carefully before they’re viewed as gospel – but this is a scary number. Aren’t reducing innings and pitches during the season supposed to protect relief pitchers’ arms?

I have argued that pitchers often throw harder when they move to the bullpen, and that this extra velocity places more stress on the UCL. In that same time period (2007, to 2016), relief pitchers threw their average fastball at a velocity of 91.5 +/- 3.35 mph, and starters threw their fastball at an average speed of 90.7 +/- 2.6 mph. Maybe, just maybe – those back to back to back appearances that relievers can make are worse for their bodies than the 6 innings pitched every 5 days?

Anyway – let’s move on to the workload metrics since 2007!

Starters

Team Workloads

The 2011 Rays take the cake for total workload for starting pitchers. Lead by David Price and Big Game James Shields, the Rays starters were not only good – they worked hard in the 2011 season. Overall, the highest average workload belonged to the tigers – particularly in 2014 and 2015 seasons.

Individual Workloads

The highest workload for a starting pitcher belongs to Justin Verlander in 2011. In fact, it is alarming to see just how many times Verlander and Sabathia’s names show up in the top 25 of this list. Those guys were horses in their prime – and it’s unknown how those huge workloads contributed to both of their recent injury problems. Conversely – how much of their durability during that time was because they worked so much, and had great pitching fitness?

Relief Pitchers

Bullpen Averages

The Rockies 2012 bullpen put in the most about of work during the past ten years. This was a direct result of a really bad starting rotation – only one pitcher cleared 100 innings pitched. The relief core was totally hung out to dry on this team. Overall, the Nationals had the highest yearly workload average for their bullpen (though this is driven by the late 2000’s when they were not very good).  There is a general trend for bullpen workloads to increase in the past 10 years – with 2015 having the highest workload for relievers in that time frame.

Individual Workloads

At first glance, I have to say – these numbers looked just… wrong. Then, I looked again – and they didn’t change.

Francisco Rodriguez put up an INSANE workload in 2010 – 62.84 – with nearly 1800 pitches, and over 100 innings. That’s a lot of exposure to high pressure situations, back to back days, and pitches per inning. The set up men, and the swing men – those who pitch more than an inning in relief, appear to have the highest workload levels. Something else that came up this weekend – was the topic of Dellin Bettances. After giving up a walk off in his third day of work in three days, people talked about his over use with the Yankees. In the past 3 years – no one has a higher workload than Bettances.

You are welcome to question the FU’s! Hit me up at michaelsonne@gmail.com, or on Twitter @DrMikeSonne if you want to debate these findings!

The dudes over at Driveline gave us scientists the best present we could ever hope for – data. They tested out the new Bauerfeind EpiTrain Powerguard to see if it was effective in reducing elbow stress. To test out the device, they paired it with the Motus Throw Sensor – a device designed to measure stress on the elbow. This device has been tested in the field by Dr. Bryan Cole, and you can find the results over at Beyond the Box Score.

Up here in Toronto, you can’t go 5 minutes into a Blue Jays conversation without hearing about the dilemma the team faces regarding Aaron Sanchez. The young ace Sanchez, is without a doubt, the best pitcher on the team, and arguably one of the top 5 starting pitchers in the American League this season. Last year the Jays spent a ton of prospect capital to go out and get an ace in the trade market – this year, they’re talking about moving the Ace they already have into the bullpen.

Aaron Sanchez. Look at him. He’s perfect in every way. Long live Sanchez! (photo – PETER LLEWELLYN/USA TODAY Sports)

I’m not convinced that this is going to work to reduce stress on Aaron’s arm. Will he throw fewer innings? For sure – but as I’ve tried to demonstrate – fatigue accumulation in the arm doesn’t necessarily depend on the number of innings you pitch, but more on the number of pitches you throw in an inning. Sanchez has been known to dial up his fastball to 100mph out of the bullpen, and this left me asking the question – despite limiting his innings, is Aaron Sanchez going to be exposing his arm to more stress by throwing out of the pen? (From Brook’s Baseball – in 2016, Sanchez’s sinker has averaged 95.26 mph, compared to 97.1 mph in September of 2015 – when Sanchez was used as a reliever). Let’s look at the driveline data to see if we can figure this out.

In the driveline study, 5 pitchers threw 20 pitches each. Some had Powerguard on, some didn’t – but for the sake of this study, I’m going to ignore that factor (they didn’t find there was a reduction in stress, anyway). First, I looked at the relationship between stress and the other variables that came out of the Motus Throw Sensor. There was an R2 of 0.84 between pitch velocity and elbow stress – that means, 84% of the stress on the UCL can be accounted for by the velocity of the pitch. If someone throws harder – they’re going to have more elbow torque, and greater UCL stress. The rest of the variables – they get a bit hazier.

Peak UCL Stress vs. Pitch Velocity – from 5 pitchers, throwing 20 times each. The UCL stress is calculated from the MotusThrow Sensor.

Arm speed has an inverse relationship with elbow torque. Greater arm speeds appear to have less UCL stress, but arm speed only accounts for 25.5% of the variance in UCL stress (an R2 of 0.25). Arm slot accounted for none of the variance in UCL stress (so no fancy graph for this one). Finally, shoulder rotation angle accounted for 34.8% of the variance in UCL Stress. I’m not entirely sure what “shoulder rotation angle” is defining here, so I’m just going to leave it for now. Essentially, with a greater shoulder rotation angle, there is greater UCL stress.

UCL Stress vs. Arm Speed (in angles per second), calculated from the MotusThrow Sensor.

UCL Stress vs. Shoulder Rotation, calculated from the MotusThrow Sensor.

The idea that UCL injuries are more prevalent in higher velocity pitchers is not a new one (Keller et al., 2016). Researchers from the University of Michigan found that one of the most significant predictors for elbow injury was ball speed (Whiteside et al., 2016). However, how does a change in ball speed influence UCL stress?

I used the driveline data, and I rank ordered UCL stress, and Velocity. So – there is a 1 through 20 for Velocity and Stress – which I’ll refer to as individual velocity and individual stress. I then ran a Spearman’s correlation on these data.

Ranked intra-pitcher UCL stress compared to ranked intra-pitcher pitch velocity.

There was an R2 of 0.17 – essentially stating that an internal increase of velocity is associated with 17% of the increase in UCL stress. As you can see in this graph, this is not the strongest of relationships. Does a pitcher ramping up and throwing harder, within his own capacities increase stress on the arm? Possibly, but I don’t think it’s that clear.

There are a lot of other factors that go into determining how stress may change between the role of a starter and a reliever. Particularly, relievers (and relievers in the proposed role that Sanchez will fill) will be coming in for high leverage situations. Working in such a stressful situation can change kinematics, as Bill Marras’ group found when exposing those who were lifting boxes to highly stressful work environments (Marras et al., 2000). When preventing injury, recovery is one of the most important aspects of health. Relief pitchers can perform on up to three consecutive days – and while pitching only 1 inning at a time (in most cases), they still need to perform warm up pitches. Their workload is definitely different than a starter’s, but I don’t think there is enough evidence out there to support that switching from a starting role to a reliever’s role is that much of a reduction in demands on the arm.

The Blue Jays hired a high performance team to help make scientific decisions when it comes to things like monitoring a pitcher’s workload. They have a really hard decision ahead of them, and the long term health of Aaron Sanchez depends on them making the right choices.

References

Marras, W. S., Davis, K. G., Heaney, C. A., Maronitis, A. B., & Allread, W. G. (2000). The influence of psychosocial stress, gender, and personality on mechanical loading of the lumbar spine. Spine, 25(23), 3045-3054.

Keller, R. A., Marshall, N. E., Guest, J. M., Okoroha, K. R., Jung, E. K., & Moutzouros, V. (2016). Major League Baseball pitch velocity and pitch type associated with risk of ulnar collateral ligament injury. Journal of Shoulder and Elbow Surgery, 25(4), 671-675.

Whiteside, D., Martini, D. N., Lepley, A. S., Zernicke, R. F., & Goulet, G. C. (2016). Predictors of Ulnar Collateral Ligament Reconstruction in Major League Baseball Pitchers. The American journal of sports medicine, 0363546516643812.

In the bottom right corner of your screen, you see the number of outs, you see the score of the game, the inning number, and right at the top of that ticker – the number of pitches that the pitcher has thrown (Figure 1).

Figure 1. Tickers from various broadcasts, illustrating a bunch of information to make you feel more informed.

Pitch counts have been used as a metric to measure workload in pitchers for some time now. Broadcasters constantly speculate on when a starter will be removed from a game as they approach that insidious 100 pitch limit – but is it just as simple as counting up the number of times that a ball has been thrown?

Zack Rymer found those pitchers who averaged 100 pitches per start were not more likely to get injured. Tom Karakolis and his crew pointed to the same findings – pitch counts or innings pitched may not be the best method of measuring workload.

Earlier this season, Ross Stripling was pulled from a no-hitter because he came up against the 100 pitch limit. This limit, while based on an article by Whiteside and colleagues (Whiteside et al., 1999), does ignore the fact that throwing 100 pitches over a complete game is probably going to be a lot less stressful than pounding through 100 pitches over 5 innings. Dieter Kurtenbach (@dkurtenbach) wrote a great article surrounding the mystique of the 100 pitch limit, and illustrated a few other workload measures (like the pitcher abuse points). The main point from this article, is that all pitches cannot be considered equal, and drawing a hard line in the sand at 100 is probably not going to save elbows, or preserve young pitchers.

Using the same fatigue model that was used to show Pitch Clocks are going to elevate muscle fatigue in pitchers, I wanted to show how the 100 pitch limit is probably not our best metric for evaluating stress in pitchers.

Fatigue Modeling

The fatigue model I used for this analysis is published in the Journal of Ergonomics (Sonne & Potvin, 2016), and has been used to estimate fatigue levels in baseball pitchers. This model is based off of motor unit physiology. From Wikipedia:

“A motor unit is made up of a motor neuron and the skeletal muscle fibers innervated by that motor neuron’s axonal terminals. Groups of motor units often work together to coordinate the contractions of a single muscle; all of the motor units within a muscle are considered a motor pool”.

When a motor unit fires, all of the muscle fibres it innervates contract, and this causes a force to be generated. Motor units can be quite small and generate small amounts of force, or quite large and generate lots of force. At the same time, the amount of force that a motor unit can generate is impacted by the fatigued state that it is in. If a motor unit is exhausted, it cannot generate any force, and it will rely on other motor units to pick up the slack on its behalf. The order in which motor units join the good fight of force production is best described by the size principle, originally hypothesized by Henneman et al., (1965). The size principle states that smaller, less forceful motor units will be recruited first, and larger, more forceful motor units will be recruited once they are required.

We could talk about motor unit physiology for days and days, but I kind of want to write about baseball now.

The fatigue model I’m using defines fatigue as “a loss of force generating capacity”. If your muscle is 10% fatigued, that means, it can now generate only 90% of it’s pre-fatigued force. When you’re exercising, failure can occur once you’ve reach a certain amount of fatigue. From an injury perspective, the muscles used to protect your joints during movement can become fatigued, and lose some of their protective capacity.

So, to drive the model, I used the muscle demands of the forearm seen during the throwing of fastballs (DiGiovine et al., 1992, Glousman et al., 1992, Hamilton et al., 1996 Sisto et al., 1986) (Figure 2).

Figure 2. Muscle Activation levels, broken down by phase of throw, and grouped by individual forearm muscles.

I then assumed an average amount of rest between pitches (as per FanGraphs – the value used was 22.6 seconds). I assumed 2:30 of rest between innings, and simulated the offensive half of an inning as being 17 pitches long, with 22.6 of rest between each pitch.

To examine the effect of the 100 pitch limit, I simulated starts ranging between 4 and 9 innings, throwing only fastballs, but having the appropriate average of pitches per inning to get to that limit (4 inning start – 25 pitches per inning, 5 inning start – 20 pitches per inning, etc (I rounded to the nearest whole pitch). While I have calculated fatigue for individual muscles, I’m just going to graph out the average fatigue for all forearm muscles (for ease of viewing – Figure 3).

Figure 3. Average forearm muscle fatigue during starts of 4 to 9 innings, all with the same pitch count (100 pitches).

The major take home from this figure should be how high each of those lines gets on the Y Axis – the greener the line, the more innings per start – and more importantly, less fatigue per start. Chances are, if your starter has gone through 100 pitches in their first four innings, they’re likely going to get the hook. For the sake of this exercise, let’s take a look at how fatigue would change with respect to those 4, 25 pitch innings.

Figure 4. Change in fatigue compared to 4 inning start with 100 pitches – positive values indicate the level of fatigue reduction (ie, 5% represents 5% less fatigue when compared to the 4 inning start – a higher value means there is a greater benefit for fatigue reduction when throwing fewer pitches per inning).  

A quality start is defined as 6 innings pitched, allowing 3 ER or less. If a pitcher throws 100 pitches in those 6 innings, they’ll see nearly 10% less fatigue in their forearm muscles when compared to a 4 inning start. Looking at a 100 pitch, complete game start, there is a benefit of nearly 20% compared to that 4 inning start. To see the benefits in individual forearm muscles, check out table 1.

Table 1. Fatigue levels in individual forearm muscles, and the improvement in fatigue compared to a 4 inning, 25 pitch start.

So, what does this all mean? A 100 pitch limit is rooted in science, but looking at pitch counts alone in the start do tend to miss the bigger picture – the amount of work done in an individual inning appears to induce more fatigue than looking at the total pitches performed in a start alone. Working deep into games and limiting the pitches in each inning is the most effective way of keeping muscle fatigue levels low.

Effective tools for fatigue monitoring are essential to pitcher health. If you’re looking for more insight into the topic, I highly recommend following guys like Ryan Faer and Kyle Boddy on Twitter. If you’re a coach and want to look at tools to measure workload in pitchers, a great place to start is this guide from the Baseball Performance Group.

If you want to learn more about the fatigue modeling process – check out the paper I wrote for the Journal of Sports Sciences here. I’m not saying use sci-hub to download it… but I’m also not saying not to.

References

DiGiovine, N. M., Jobe, F. W., Pink, M., & Perry, J. (1992). An electromyographic analysis of the upper extremity in pitching. Journal of Shoulder and Elbow Surgery, 1(1), 15-25.

Glousman, R. E., Barron, J., Jobe, F. W., Perry, J., & Pink, M. (1992). An electromyographic analysis of the elbow in normal and injured pitchers with medial collateral ligament insufficiency. The American Journal of Sports Medicine, 20(3), 311-317.

Hamilton, C. D., Glousman, R. E., Jobe, F. W., Brault, J., Pink, M., & Perry, J. (1996). Dynamic stability of the elbow: electromyographic analysis of the flexor pronator group and the extensor group in pitchers with valgus instability. Journal of Shoulder and Elbow Surgery, 5(5), 347-354.

Henneman, E., Somjen, G., & Carpenter, D. O. (1965). Functional significance of cell size in spinal motoneurons. Journal of neurophysiology,28(3), 560-580.

Sisto, D. J., Jobe, F. W., Moynes, D. R., & Antonelli, D. J. (1987). An electromyographic analysis of the elbow in pitching. The American journal of sports medicine, 15(3), 260-263.

Sonne, M. W., & Keir, P. J. (2016). Major League Baseball pace-of-play rules and their influence on predicted muscle fatigue during simulated baseball games. Journal of sports sciences, 1-9.

Sonne, M. W., & Potvin, J. R. (2016). A modified version of the three-compartment model to predict fatigue during submaximal tasks with complex force-time histories. Ergonomics, 59(1), 85-98.

Acknowledgements – Thanks to Daanish Mulla for his help with data processing, and Patsy Sonne for her helping hand.

Introduction

Muscle fatigue is a process that results in decreased force generating capacity, and impaired performance [1]. Reduced force due to muscle fatigue may result in less stable joints, which can increase the risk of injury [2].  Furthermore, muscle fatigue is known to reduce joint proprioception  [3]–[6], which can result in further compromised joint stability and increased injury risk. Baseball pitchers have been shown to alter their kinematics (joint angles) when fatigued, which may strain different tissues when compared to pitching without fatigue [7].  Repetitive strain on these tissues can result in injury, and in baseball pitchers, injuries such as Ulnar Collateral Ligament tear.

Fatigue has been named the number one cause of injuries in baseball pitchers, leading to a 500% increase in injury likelihood [8]. Handgrip strength has decreased by up to 5% after simulated baseball games [9], and pitch velocity decreases over the the course of a game [10]. Pitcher kinematics also change with fatigue, with the elbow dropping lower, and the stride getting shorter.

The PITCHf/x system was created by Sportvision, and installed in every MLB stadium since 2006. The system allows for tracking of pitch movement, velocity and release point for every pitch thrown at the major league level. Two cameras are mounted in each stadium, and are used to track each pitch and display data during live broadcasts and websites. With the use of free software, like the programming package R, and database software MySQL, anyone can download gigabytes of data within hours, allowing for detailed analyses of pitching and hitting. With this detailed data, it would theoretically be possible to track changes associated with muscle fatigue. The purpose of this study was to examine how pitch velocity and release point changed in starting pitchers during the 2015 season.

Methods

Data Acquisition

I queried the pitchFX data from the 2015 season, grouping pitches by pitch type, pitcher, and inning. A pitch had to be thrown 20 times in an inning to be included for further analysis. The pitchers included in this analysis were those who pitched a minimum of 100 innings as a starting pitcher. The main focus of this analysis was to examine peak velocity changes, so only fastball type pitches were included in the analysis (four-seam, two-seam, split finger, sinking, cut, and general fastball).

I calculated the average velocity for each pitcher during their first inning of pitching. I then calculated the minimum average velocity for these pitches during either the 5^th, or 6^th inning – which ever value was the lowest.

For release point, I calculated the resultant distance of the release point (at z0, x0), from 0.0 (Figure 1). I also examined the change in vertical release point (z0) between the first inning, and the minimum of the 5^th and 6^th innings. Using the horizontal release point, and the vertical release point, I also calculated the absolute release angle (normalizing for left-handed and right-handed pitchers).

Figure 1. Demonstration of how calculations were made for the vertical release point, resultant release distance, and release angle.

Statistics

For this analysis, the independent variable was inning (first inning, minimum of 5^th/6^th inning).

To examine the effect of inning, I performed a dependent samples t-test on variables of peak velocity, resultant release point, vertical release point, and release angle, with p < 0.05. I also calculated Cohen’s D to determine the effect size of the inning.

Results

Peak velocity significantly decreased between the first inning (91.19 ± 2.91 mph) and 5^th/6^th inning of the start (90.61 ± 3.01 mph, p< 0.05; d=0.20) (Figure 2). Vertical release point significantly decreased from 5.9 ± 0.35 feet to 5.84 ± 0.36 feet (p < 0.05, d=0.17)(Figure 3a). Resultant release point also decreased from 6.15 ± 0.35 feet to 6.09 ± 0.35 feet (p < 0.05, d=0.18) (Figure 3b). All of these changes were statistically significant, however, represented small effect sizes.

Release angle was significantly different between the first and final inning, moving from 74.9 ± 6.17 degrees to 75.1 ± 6.31 degrees. This represents a release angle that is closer to the vertical plane, or, closer to the midline of the body. While this change was statistically significant, the effect size was negligible (d=-0.04) (figure 4).

Figure 2. Fastball velocity significantly decreased between the first inning (91.19 ± 2.91 mph) and the minimum between the 5th and 6th inning (90.61 ± 3.01 mph) (p < 0.05). This represented a small effect size, of 0.20.

Figure 3. Both vertical release point, and resultant release distance decreased between the first inning and the 6th inning, representing a possible change in pitcher kinematics. This represented a small effect size, of 0.18 and 0.17, respectively.

Figure 4. Release angle increased (representing a release point closer to the midline of the body) between the first and final inning, though the effect size for this relationship was negligible.

Discussion

In line with previous research on baseball pitching and fatigue, fastball velocity decreased between the beginning and the end of the average game. A decrease in release point distance and height also indicates that kinematics have changed during the course of a baseball game.

The following examples are from pitchers in the top ten for fatigue related changes between innings. Andrew Heaney has a nearly 2mph decline between the 1^st and the 6^th inning (Figure 5a), and Ervin Santana has his resultant release point decrease by 2.21% (Figure 5b). In both cases, it could be expected that performance would be impaired by these fatigue related changes. Conversely, Jacob deGrom actually increases his release point by 0.58% (Figure 5d), and Max Scherzer increases fastball velocity by 0.38% between the first and 6^th inning (figure 5c). In general, 70% of pitchers experience a decreased velocity between the first and final inning, 85% of pitchers have a decrease in their resultant release point, and 83% of pitchers have a decrease in their vertical release point.

Figure 4. Release angle increased (representing a release point closer to the midline of the body) between the first and final inning, though the effect size for this relationship was negligible.

The velocity change demonstrated in this analysis represents a decrease of only 0.5 mph from the first to the 6^th inning. This represents approximately a 1% change in velocity. Previous research has shown up to a 5mph decrease in velocity, decreasing from 90 mph to 85 mph during spring training games [10]. This greater decrease in velocity may represent decreased conditioning from the pitchers at this time of the season. Crotin, et al., [11] found that fastball velocity increased during a season, as a result of conditioning and improved strength. These factors may wash out some of the differences that could be seen throughout the course of a game, when average velocities are calculated over the course of an entire season and by inning, like in this analysis.

The pitchers included in this analysis represent a highly elite subset of the population. Previous research that has examined fatigue in baseball pitchers has included pitchers in spring training [10], college [9], or even Japanese high school players [12]. The fatigue effects for the elite population may not be as severe, as elite athletes are able to moderate the detrimental effects of fatigue when performing their sport specific task [13].

Limitations

Despite the easy access to PitchFX data, there are concerns with the accuracy and reliability of the system. For one, the release point displayed by the PitchFX system is at a distance of 50 feet from the plate. Typically, pitchers release the ball at 54-55 feet from the plate, so the true release point is not exactly known [14] Additionally, inter-stadium differences may also contribute to inaccurate PitchFX data – as cameras are not always in the exact same place in all stadiums.

Conclusions

Examining PitchFX data for fastball velocities and release points, averaged by inning for qualifying starters in the 2015 season, have produced results comparable to more controlled, lab based studies, on fatigue during pitching. However, limitations with the PitchFX system, and averaging data throughout the entire season can possibly remove some of the differences that could possible be seen as a pitcher fatigues. Additional research should be performed to examine in-game changes in velocity for both good, and bad starts, to see if fatigue effects are more prominent as a pitcher becomes less effective.

References

[1]       R. M. Enoka and J. Duchateau, “Muscle fatigue: what, why and how it influences muscle function.,” J. Physiol., vol. 586, no. 1, pp. 11–23, Jan. 2008.

[2]       G. S. Fleisig, J. R. Andrews, C. J. Dillman, and R. F. Escamilla, “Kinetics of baseball pitching with implications about injury mechanisms,” Am. J. Sports Med., vol. 23, no. 2, 1995.

[3]       L. A. Hiemstra, I. K. Lo, and P. J. Fowler, “Effect of fatigue on knee proprioception: implications for dynamic stabilization.,” J. Orthop. Sports Phys. Ther., vol. 31, no. 10, pp. 598–605, Oct. 2001.

[4]       F. Ribeiro, J. Mota, and J. Oliveira, “Effect of exercise-induced fatigue on position sense of the knee in the elderly,” Eur. J. Appl. Physiol., vol. 99, no. 4, pp. 379–385, 2007.

[5]       M. Sharpe and T. Miles, “Position sense at the elbow after fatiguing contractions,” Exp. Brain Res., vol. 94, no. 1, May 1993.

[6]       H. B. Skinner, M. P. Wyatt, J. A. Hodgdon, D. W. Conrad, and R. . Barrack, “Effect of fatigue on joint position sense of the knee,” J. Orthop. Res., vol. 4, no. 1, pp. 112 – 118, 1986.

[7]       R. F. Escamilla, S. W. Barrentine, G. S. Fleisig, N. Zheng, Y. Takada, D. Kingsley, and J. R. Andrews, “Pitching biomechanics as a pitcher approaches muscular fatigue during a simulated baseball game.,” Am. J. Sports Med., vol. 35, no. 1, pp. 23–33, Jan. 2007.

[8]       J. Lemire, “Preventing Athlete Injuries With Data-Driven Tech – Athletic Business,” Athletic Business, 2015. [Online]. Available: http://www.athleticbusiness.com/athlete-safety/preventing-athlete-injuries-with-data-driven-tech.html. [Accessed: 21-Dec-2015].

[9]       M. J. Mullaney, “Upper and Lower Extremity Muscle Fatigue After a Baseball Pitching Performance,” Am. J. Sports Med., vol. 33, no. 1, pp. 108–113, Jan. 2005.

[10]     T. a Murray, T. D. Cook, S. L. Werner, T. F. Schlegel, and R. J. Hawkins, “The effects of extended play on professional baseball pitchers.,” Am. J. Sports Med., vol. 29, no. 2, pp. 137–42, 2001.

[11]     R. L. Crotin, S. Bhan, T. Karakolis, and D. K. Ramsey, “Fastball velocity trends in short-season minor league baseball.,” J. Strength Cond. Res., vol. 27, no. 8, pp. 2206–12, Aug. 2013.

[12]     L.-H. Wang, K.-C. Lo, I.-M. Jou, L.-C. Kuo, T.-W. Tai, and F.-C. Su, “The effects of forearm fatigue on baseball fastball pitching, with implications about elbow injury.,” J. Sports Sci., pp. 1–8, Oct. 2015.

[13]     M. Lyons, Y. Al-Nakeeb, and A. Nevill, “The impact of moderate and high intensity total body fatigue on passing accuracy in expert and novice basketball players.,” J. Sports Sci. Med., vol. 5, no. 2, pp. 215–27, Jan. 2006.

[14]     M. Fast, “The Internet cried a little when you wrote that on it – The Hardball Times,” The Hardball Times, 2010. [Online]. Available: http://www.hardballtimes.com/the-internet-cried-a-little-when-you-wrote-that-on-it/. [Accessed: 21-Dec-2015].